What's up guys! Akhirnya minggu minggu final exam sudah lewat, as i promise to you guys! kali ini gue bersemangat banget untuk ngeposting materi tentang persamaan dan pertidaksamaan nilai mutlak! Check this out! Keep calm and stay learning math!
Persamaan dan Pertidaksamaan Nilai Mutlak
A. Nilai Mutlak
Nilai mutlak adalah jarak pada garis bilangan real antara bilangan yang dimaksud dengan dengan nol.
untuk  bilangan real didefinisikan
bilangan real didefinisikan 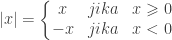
Contoh:
B. Persamaan Nilai Mutlak
Sifat-sifat nilai mutlak
, (ketaksamaan segitiga)
atau
EItss.. Sebelum you guys melihat contoh soal, harap dikerjakan sendiri dulu soal soal dibawah baru setelah itu kalian lihat pembahasan biar kalian tambah mengerti dan tahu kesalahan kalian dimana:D
Contoh Soal:
1. Tentukan nilai  yang memenuhi
yang memenuhi 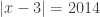
Jawab:
Jawab:
………………… 1)
……………. 2)
Dari persamaan (1) diperoleh  , dan dari persamaan (2) diperoleh
, dan dari persamaan (2) diperoleh 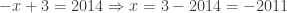 .
.
Jadi, nilai yang memenuhi adalah
yang memenuhi adalah  atau
atau 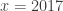
Jadi, nilai
2. Tunjukkan bahwa 
Bukti:
Bukti:
3. Tentukan nilai  yang memenuhi
yang memenuhi 
Jawab:
Jawab:
————————————————— ,masing-masing ruas dikuadratkan
4. Gambarkanlah grafik  untuk
untuk  bilangan real!
bilangan real!
Jawab :
untuk
dan seterusnya
Perhatikanlah ilustrasi berikut ini
 [sumber]
[sumber]
Soal Latihan
- Tentukan nilai dari
- Tentukan nilai dari
- Tentukanlah nilai
yang memenuhi persamaan
- Carilah harga
yang memenuhi
- Carilah harga
yang memenuhi
- Tunjukkan bahwa
- Tunjukkan bahwa
- Gambarlah grafik
- Gambarkanlah grafik
, untuk
C. Pertidaksaan Nilai Mutlak
Untuk  bilangan real dan
bilangan real dan  , maka
, maka
- Jika
, maka
Contoh Soal:
Harap kerjain soal dibawah ini dulu guys, setelah itu baru lihat pembahasannya biar kalian bisa mengukur kadar kemengertian kalian di materi ini:D
1. Tentukanlah himpunan penyelesaian dari 
Jawab:
2. Tentukan penyelesaian dari pertidaksamaan harga mutlak dari 
Jawab :
, atau
Sehingga penyelesaiannya adalah 
3. Tentukan penyelesaian pertidaksamaan harga mutlak dari 
Jawab:
, atau
Jadi, penyelesaiannya adalah 
Latihan Soal
- Penyelesaian dari pertidaksamaan
adalah ….
- Penyelesaian dari pertidaksamaan
adalah ….
- Penyelesaian dari pertidaksamaan
adalah ….
- Carilah nilai x yang memenuhi
- Himpunan penyelesaian dari pertidaksamaan
adalah ….
- Tentukan nilai x yang memenuhi pertidaksamaan
- Penyelesaian dari pertidaksamaan
adalah ….
- Penyelesaian dari pertidaksamaan
Sekian postingan dari gue, semoga bermanfaat bagi kalian. Berikutnya gue akan memposting tentang Fisika, dan Kimia. Ditunggu ya:D
Sumber Referensi
- Enung, Untung. 2009. Mandiri Matematika SMAjilid 1 Untuk Kelas X. Jakarta: Erlangga.



0 komentar:
Posting Komentar